Markov Chains

A Markov chain is a model that describes a set of transitions which are determined by some probability distribution that satisfy the Markov property.

The Markov property is that the chain must be “memory-less” meaning the probability of the transition to the next state is dependent solely on the current state and not the steps that led up to the present state.

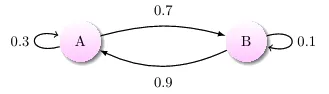
$$ P = \begin{pmatrix} 0.3 & 0.7 \\ 0.9 & 0.1 \end{pmatrix} $$

Markov chains can be described in a transition matrix which for a markov chain with N states is a NxN matrix where each element is the probability of transitioning from state i to state j.

Finding the k-th step in the transition is as easy as conditional probability of multiplying the probability of following each state or actually raising the transition Matrix M to the kth power.

$$ P^2 = \begin{pmatrix} 0.3 & 0.7 \\ 0.9 & 0.1 \end{pmatrix} * \begin{pmatrix} 0.3 & 0.7 \\ 0.9 & 0.1 \end{pmatrix} = \begin{pmatrix} 0.3 * 0.3 + 0.7 * 0.9 & 0.3 * 0.7 + 0.7 * 0.1\\ 0.9 * 0.3 + 0.1 * 0.9 & 0.9 * 0.7 + 0.1 * 0.1 \end{pmatrix} $$ $$ = \begin{pmatrix} 0.72 & 0.28\\ 0.36 & 0.64 \end{pmatrix} $$

Markov Decision Process

MDP is an extension of the Markov chain. It provides a mathematical framework for modeling decision-making situations.

MDP is an expansion of MC;

MC is a stone rolling down the road and has a probability at each fork in its path to go left or right.

MDP is when you put someone (agent) on the stone that tries to or has the ability to affect the stone’s path and steer it a bit to the left or the right. This means that the probability of the stone actually veering to the left or the right is dependent upon the action that the agent takes.